The Kalman filter is a very useful algorithm in time series analysis - but can be daunting on a first viewing. The most famous application of the Kalman filter was by the NASA Ames Research Center in the 60s to construct a navigation system for the Apollo space capsule. Since then it has been used in the aerospace industry extensively and most recently in finance and economics. This post aims to make the filter less daunting by showing where the key equations come from under the assumption of gaussian errors. We will then give a simple implementation of the algorithm in R.
To use the Kalman filter we must write our time series model in the following form below.
For
To use the Kalman filter we must write our time series model in the following form below.
For
Measurement equation
Initial condition
The measurement equation describes how the observed variable  is determined. The state equation describes how the unobserved state variable
is determined. The state equation describes how the unobserved state variable  is determined. The vectors
is determined. The vectors 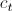 and
and are vectors of exogenous variables.
are vectors of exogenous variables.
 is determined. The state equation describes how the unobserved state variable
is determined. The state equation describes how the unobserved state variable  is determined. The vectors
is determined. The vectors 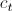 and
and are vectors of exogenous variables.
are vectors of exogenous variables.
For convenience let us define
The Kalman filter can be broken down into the following steps:
1. Prediction
2. Measurement
3. Correction
Prediction step
Suppose we have our final estimate of alpha given all available at the end of period t-1. Then before taking our new measurement we can make predictions for alpha and the new measurement. These predictions are calculated by the following equations - which can be obtained by applying the expectation operator to the state and measurement equations respectively.
we can make predictions for alpha and the new measurement. These predictions are calculated by the following equations - which can be obtained by applying the expectation operator to the state and measurement equations respectively.
 we can make predictions for alpha and the new measurement. These predictions are calculated by the following equations - which can be obtained by applying the expectation operator to the state and measurement equations respectively.
we can make predictions for alpha and the new measurement. These predictions are calculated by the following equations - which can be obtained by applying the expectation operator to the state and measurement equations respectively.
Using our earlier definitions, the associated MSE for these predictions are given by
and
Measurement step
This prediction error provides us with information regarding the accuracy of our initial estimate of alpha.
Correction step
Given the assumption of independent identically distributed gaussian errors we have
Using the following property of the multivariate gaussian distribution
If
Then
Where
We can obtain the correction equations for the Kalman filter.
where
These final estimates can then be used in the prediction step to make new predictions of alpha and y at date t+1.
Intuition
Consider the first equation, the intuition is pretty straightforward. The equation roughly says that the final estimate of is our previous estimate before making our measurement plus the prediction error using our initial estimate scaled by the Kalman gain. The Kalman gain can be interpreted as gauging the information contained in our new measurement. The larger the Kalman gain, the more weight will be given to our new measurement and conversely the smaller the Kalman gain, the less weight given. Note if the prediction error is zero then we should not change our estimate of
is our previous estimate before making our measurement plus the prediction error using our initial estimate scaled by the Kalman gain. The Kalman gain can be interpreted as gauging the information contained in our new measurement. The larger the Kalman gain, the more weight will be given to our new measurement and conversely the smaller the Kalman gain, the less weight given. Note if the prediction error is zero then we should not change our estimate of . The second equation describes the evolution of the MSE of our estimate of the state vector. We can see that the MSE of our estimate is also reduced hence our uncertainty regarding the value of alpha is smaller.
. The second equation describes the evolution of the MSE of our estimate of the state vector. We can see that the MSE of our estimate is also reduced hence our uncertainty regarding the value of alpha is smaller.
 is our previous estimate before making our measurement plus the prediction error using our initial estimate scaled by the Kalman gain. The Kalman gain can be interpreted as gauging the information contained in our new measurement. The larger the Kalman gain, the more weight will be given to our new measurement and conversely the smaller the Kalman gain, the less weight given. Note if the prediction error is zero then we should not change our estimate of
is our previous estimate before making our measurement plus the prediction error using our initial estimate scaled by the Kalman gain. The Kalman gain can be interpreted as gauging the information contained in our new measurement. The larger the Kalman gain, the more weight will be given to our new measurement and conversely the smaller the Kalman gain, the less weight given. Note if the prediction error is zero then we should not change our estimate of . The second equation describes the evolution of the MSE of our estimate of the state vector. We can see that the MSE of our estimate is also reduced hence our uncertainty regarding the value of alpha is smaller.
. The second equation describes the evolution of the MSE of our estimate of the state vector. We can see that the MSE of our estimate is also reduced hence our uncertainty regarding the value of alpha is smaller.
Lets take a look at a simple application of the Kalman filter.
Example
Consider the local level model.
Measurement equation
where
This can be found by choosing
We simulate some data from this model in R and implement the Kalman filter algorithm to obtain recursive estimates of alpha. Because alpha is non-stationary we choose a diffuse prior i.e. draw from a normal with mean equal to the unconditional mean of alpha and a large variance for our starting value of alpha.
# local level model
# measurement eq: yt = alphat + et
# state eq: alphat = alphat_1 + nt
# assume et is iidN(0,H)
# assume nt is iidN(0,Q)
# assume initial state alpha0 is N(a0,P0)
# initial conditions
a0 <- 0
P0 <- 10^6
# choose number of observations
n <- 250
# generate data
H <- 10
Q <- 0.01
alpha0 <- rnorm(a0,sqrt(P0))
alpha0 <- rnorm(a0,sqrt(P0))
eta <-rnorm(n, mean = 0,sd = sqrt(Q))
alpha <- cumsum(eta)
epsilon <- rnorm(n, mean = 0, sd = sqrt(H))
y <- alpha + epsilon
# define variables
a.tt_1 <- rep(0,n)
y.tt_1 <- rep(0,n)
a.tt <- rep(0,n)
P.tt_1 <- rep(0,n)
P.tt <- rep(0,n)
Kt <- rep(0,n)
a.tt[1] <- a0
y.tt_1[1] <- a.tt[1]
P.tt_1[1] <- P0
# start filter
for(i in 2:n) {
# calculate initial guess of alphat based on all information from t_1
a.tt_1[i] <- a.tt[i-1]
# predicted yt given all information from t_1
y.tt_1[i] <- a.tt_1[i]
# calculate MSE of initial guess of alphat based on info from t_1
P.tt_1[i] <- P.tt[i-1] + Q
# calculate the Kalman filter for date t
Kt[i] <- P.tt_1[i] * (P.tt_1[i] + H)^(-1)
# combine prediction of yt with actual yt and initial guess of alpha t to obtain
# final estimate of alphat and the associated MSE for that estimate
a.tt[i] <- a.tt_1[i] + Kt[i] * (y[i] - y.tt_1[i])
P.tt[i] <- (1 - Kt[i]) * P.tt_1[i]
}
#collect results
alpha <- ts(alpha, start = 1, end = n, freq = 1)
a.tt <- ts(a.tt, start = 1, end = n, freq = 1)
y <- ts(y, start = 1, end = n, freq = 1)
data <- cbind(alpha,a.tt,y)
# plot results
plot.ts(data, plot.type = c("single"), xlab = "iteration", ylab = "", lty = c(1,1,2), col = c("blue", "red", "green"), type = "l")
legend("topright", legend = c("true", "estimate", "measurement"), col = c("blue", "red", "green"), lty = c(1,1,3), bg = "white")
Note that we assumed the variances H and Q were known. In practice we would have to estimate these parameters using the data. The Kalman filter provides us with a way to form the likelihood and perform QMLE. I will address the problem of parameter estimation in Pt.2.































No comments:
Post a Comment