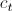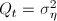Kalman filter pt.2 - Parameter estimation

In part one, I gave an overview of the Kalman filter and used R to simulate some data from the local level model (given below as a reminder) and apply the filter. However, when applying the filter I assumed the variances $\sigma_{\epsilon} ^2$ and $\sigma_{\eta} ^2$ were known. In this post we'll show that the Kalman filter also provides a useful way of constructing the log likelihood function and consequently obtaining the MLE of the variances.

Local level model

Measurement equation

State equation

where

To carry out MLE of the parameters we must form the log likelihood function. In time series analysis observations are typically not independent so to write the likelihood function, the standard approach is to use the prediction-error decomposition of the likelihood function. This done by factorizing the joint-density into a a product of conditional density functions.

For example, suppose we have three observations $y_1,y_2,y_3$

Then

$f(y_1,y_2,y_3) = f(y_3|y_2,y_1)f(y_2,y_1)$

$= f(y_3|y_2,y_1)f(y_2|y_1)f(y_1)$

In general for T observations we have

$L(y_1,y_2,...,y_T;\theta) = (\prod_{t=2}^{T}\ f(y_t|y_{t-1},..y_1))f(y_1)$

$= (\prod_{t=2}^{T}\ f(y_t|I_{t-1}))f(y_1)$

Where $I_t$ denotes all available information at date t.

Now recall from last time we had the following result

where implicit in the notation we have conditioned on all available information at date t-1.

which implies

Now define

Then the log likelihood function is given by

$L(\theta | y_1,..y_T; a_0, P_0) = $

$- \frac{nT}{2}ln(2\pi) - \frac{1}{2} \sum_{t=1}^{T} (ln|F_t(\theta)| + v_t(\theta)'F_t(\theta)^{-1}v_t(\theta))$

Which can then be maximised numerically with respect to the unknown parameters $\theta$. 

Example

The R code below generates data from the local level model and estimates the variances by QMLE.

# local level model

# observation eq: yt = alphat + et

# state eq: alphat = alphat_1 + nt

# assume et is iidN(0,H)

# assume nt is iidN(0,Q)

# assume initial state alpha0 is N(a0,P0)

# initial conditions

a0 <- 0

P0 <- 10^6

# choose number of observations

n <- 250

# generate data 

set.seed(1234)

H <- 10

Q <- 0.01

eta <-rnorm(n, mean = 0,sd = sqrt(Q))

alpha <- cumsum(eta)

epsilon <- rnorm(n, mean = 0, sd = sqrt(H))

y <- alpha + epsilon 

#construct the negative loglikelihood function

neg.logl <- function(y,a0,P0,theta) {

#create variables

H <- exp(theta[1])

Q <- exp(theta[2])

#note we have reparameterized the variance to avoid the problem of negative estimates of the variances

n <- length(y) 

a.tt_1 <- rep(0,n)

y.tt_1 <- rep(0,n)

v.tt <- rep(0,n)

a.tt <- rep(0,n)

P.tt_1 <- rep(0,n)

P.tt <- rep(0,n)

F.tt_1 <- rep(0,n)

Kt <- rep(0,n)

lht <- rep(0,n)

a.tt[1] <- a0

y.tt_1[1] <- a.tt[1]

P.tt_1[1] <- P0

# start filter

for(i in 2:n) {

# calculate initial guess of alphat based on all information from t_1

  a.tt_1[i] <- a.tt[i-1]

# predicted yt given all information from t_1, and calculate the prediction error

  y.tt_1[i] <- a.tt_1[i]

  v.tt[i] <- y[i] - y.tt_1[i]

# calculate MSE of initial guess of alphat based on info from t_1

  P.tt_1[i] <- P.tt[i-1] + Q

  F.tt_1[i] <- P.tt_1[i] + H

# calculate the Kalman gain for date t

  Kt[i] <- P.tt_1[i] * (F.tt_1[i])^(-1)

# combine prediction of yt with actual yt and initial guess of alpha t to obtain

# final estimate of alphat and the associated MSE for that estimate

a.tt[i] <- a.tt_1[i] + Kt[i] * v.tt[i]

P.tt[i] <- (1 - Kt[i]) * P.tt_1[i]

# calculate log of the density fn for observation i

    lht[i] <- dnorm(v.tt[i], mean = 0, sd = sqrt(F.tt_1[i]), log = TRUE)

}

# calculate negative log likelihood fn

logl <- sum(lht)

return(-logl)

}

  

#estimate H and Q
#the optim() fn in R minimises the objective function which is why we calculated the negative log likelihood fn
# optim() requires starting values - which choose to use random start values

start_val <- c(runif(1),runif(1))

output <- optim(start_val, neg.logl, method = "BFGS", y=y,a0=0,P0=10^6, hessian = T)

#get results

theta <- output$par

# remember we maximised w.r.t the log of the variances thus we need to take the exp() of theta

estim <- exp(theta)

names(estim) <- c("H.estim", "Q.estim")

# calculate the variance-covariance matrix
# note we don't need to take the minus here because we already did that when constructing the negative log likelihood

V <- solve(output$hessian)


You should get approximately 11.25 and 0.023 for the MLE of H and Q respectively, which are reasonably close to their true values.

Too much math not enough intuition: undergraduate microeconomics

In any undergraduate microeconomics course, students are always expected to solve the basic consumer problem:

Nick has an income level $M$ to spend on two goods, imaginatively named, $x_1$ and $x_2$. The price of these two goods is fixed at prices $P_1$ and $P_2$ and Nick's preferences over these two goods are described by a utility function $U(x_1,x_2)$. Further, assume Nick is an extraordinarily greedy guy (technical term: Nick has locally non-satiated preferences for these two goods) and is always happier when he consumes more of $x_1$ or $x_2$, so Nick will always spend all his income.

The basic problem is how should Nick allocate his income $M$ between these two goods?

Formally, what we're really looking for is the solution to the following maths problem:

subject to

The standard approach offered to undergraduates is to solve this problem by forming the Lagrangian and then computing the first-order conditions and solving them for $x_1$ and $x_2$.

This was the approach I used throughout my undergraduate studies but I would argue this approach is very long-winded and skips over some important economic intuition. This second approach was not introduced to me till my math prep course at the start of my postgraduate studies - even though its less complicated and much more intuitive!

Ask yourself the following question: What's the opportunity cost for Nick of consuming a bundle $(x_1,x_2)$?

Well, Nick could reduce his consumption of $x_1$ by 1 unit freeing up $P_1$ units of income and allocating that additional income to buying $P_1/P_2$ units of $x_2$. Given Nick's preferences, which are represented by $U(x_1,x_2)$, the above reallocation causes his level of utility to change by

Where, $MU_1$ and $MU_2$ describe Nick's marginal utility of $x_1$, and $x_2$ respectively. 

If 

Then, Nick prefers this bundle over the old bundle, hence the old bundle can't be his most preferred bundle.

Likewise,

If

which is equivalent to

Then Nick would be better off by reducing his consumption of $x_2$ by 1 unit and buying $P_2/P_1$ units of $x_1$. Once again, his old bundle can't be his most preferred bundle.

Thus it must be the case that

which is equivalent to

Which is the same optimality condition you would get by using the Lagrangian approach. But instead of just blindly applying the maths, we got the result by asking what Nick is sacrificing given he consumes an arbitrary bundle $(x_1,x_2)$

To solve for Nick's optimal bundle we would make use of the budget constraint, giving us two equations with two unknowns which can be solved by substitution.

We can use this approach when solving macroeconomic models too.

In most macroeconomic models, they often start by assuming a representative consumer and use the Euler condition to solve the model. But the above example can be easily adapted.  Suppose the discount rate in the economy is given by $\beta$, price of a zero-coupon bond at date t expiring at date t+1 is $Q_t$, $P_1 = P_t$ , $P_2 = P_{t+1}$ are the prices of the consumption good at dates t and t+1 respectively,  and $x_1 = C_t$ and $x_2 = C_{t+1}$ denoting levels of consumption in period t and period t+1 respectively.

Then,

for all t.

  

A final example is Hotelling's rule which states that for an exhaustible resource the real rate of interest must equal the expected price change in the natural resource.  This can be derived by asking yourself the following questions: 

What is the payoff of keeping the natural resource in storage? 

Answer: $E_tP_{t+1}$, the expected price obtained tomorrow, whose present value is $E_tP_{t+1} / (1+r)$

So what payoff am I sacrificing by waiting till tomorrow?

Answer: $P_t$, the price today.

Suppose $P_t$ was higher than $E_tP_{t+1} / (1+r)$, then owners of the exhaustible resource would sell as much as possible today rather than wait til tomorrow. But this would depress the price today and increase the scarcity of the resource tomorrow. Thus the expected price obtained tomorrow would rise. This process would continue till $P_t = E_tP_{t+1} / (1+r)$.

Which can be expressed as $\Delta P^e = r$. Where $\Delta P^e$ denotes the expected change in price.

Throughout this post, all we've been doing is using the idea of opportunity cost - something which is taught in every pre-university Economics course.

Kalman filter pt.1 - it's not rocket science... is it?

The Kalman filter is a very useful algorithm in time series analysis - but can be daunting on a first viewing. The most famous application of the Kalman filter was by the NASA Ames Research Center in the 60s to construct a navigation system for the Apollo space capsule. Since then it has been used in the aerospace industry extensively and most recently in finance and economics. This post aims to make the filter less daunting by showing where the key equations come from under the assumption of gaussian errors. We will then give a simple implementation of the algorithm in R.

To use the Kalman filter we must write our time series model in the following form below.

For

Measurement equation

State equation

Initial condition

The measurement equation describes how the observed variable  is determined. The state equation describes how the unobserved state variable  is determined.  The vectors and are vectors of exogenous variables.

For convenience let us define

 

where  denotes all available information at date t-1.

The Kalman filter can be broken down into the following steps:

1. Prediction

2. Measurement

3. Correction

Prediction step

Suppose we have our final estimate of alpha given all available at the end of period t-1. Then before taking our new measurement we can make predictions for alpha and the new measurement. These predictions are calculated by the following equations - which can be obtained by applying the expectation operator to the state and measurement equations respectively.

Using our earlier definitions, the associated MSE for these predictions are given by

and

Measurement step

Suppose now we have our measurement for date t, denoted then the prediction error is given by

This prediction error provides us with information regarding the accuracy of our initial estimate of alpha.

Correction step

Given the assumption of independent identically distributed gaussian errors we have

Using the following property of the multivariate gaussian distribution

If

Then

Where

We can obtain the correction equations for the Kalman filter.

where

and Kalman gain given by

These final estimates can then be used in the prediction step to make new predictions of alpha and y at date t+1. 

Intuition

Consider the first equation, the intuition is pretty straightforward. The equation roughly says that the final estimate of is our previous estimate before making our measurement plus the prediction error using our initial estimate scaled by the Kalman gain. The Kalman gain can be interpreted as gauging the information contained in our new measurement. The larger the Kalman gain, the more weight will be given to our new measurement and conversely the smaller the Kalman gain, the less weight given. Note if the prediction error is zero then we should not change our estimate of. The second equation describes the evolution of the MSE of our estimate of the state vector. We can see that the MSE of our estimate is also reduced hence our uncertainty regarding the value of alpha is smaller.

Lets take a look at a simple application of the Kalman filter.

Example

Consider the local level model.

Measurement equation

State equation

where

This can be found by choosing

We simulate some data from this model in R and implement the Kalman filter algorithm to obtain recursive estimates of alpha.  Because alpha is non-stationary we choose a diffuse prior i.e. draw from a normal with mean equal to the unconditional mean of alpha and a large variance for our starting value of alpha.

# local level model

# measurement eq: yt = alphat + et

# state eq: alphat = alphat_1 + nt

# assume et is iidN(0,H)

# assume nt is iidN(0,Q)

# assume initial state alpha0 is N(a0,P0)

# initial conditions

a0 <- 0

P0 <- 10^6

# choose number of observations

n <- 250

# generate data 

H <- 10

Q <- 0.01
alpha0 <- rnorm(a0,sqrt(P0))

eta <-rnorm(n, mean = 0,sd = sqrt(Q))

alpha <- cumsum(eta)

epsilon <- rnorm(n, mean = 0, sd = sqrt(H))

y <- alpha + epsilon 

# define variables

a.tt_1 <- rep(0,n)

y.tt_1 <- rep(0,n)

a.tt <- rep(0,n)

P.tt_1 <- rep(0,n)

P.tt <- rep(0,n)

Kt <- rep(0,n)

a.tt[1] <- a0

y.tt_1[1] <- a.tt[1]

P.tt_1[1] <- P0

# start filter

for(i in 2:n) {

# calculate initial guess of alphat based on all information from t_1

  a.tt_1[i] <- a.tt[i-1]

# predicted yt given all information from t_1

  y.tt_1[i] <- a.tt_1[i]

# calculate MSE of initial guess of alphat based on info from t_1

  P.tt_1[i] <- P.tt[i-1] + Q

# calculate the Kalman filter for date t

  Kt[i] <- P.tt_1[i] * (P.tt_1[i] + H)^(-1)

# combine prediction of yt with actual yt and initial guess of alpha t to obtain

# final estimate of alphat and the associated MSE for that estimate

a.tt[i] <- a.tt_1[i] + Kt[i] * (y[i] - y.tt_1[i])

P.tt[i] <- (1 - Kt[i]) * P.tt_1[i]

}

#collect results

alpha <- ts(alpha, start = 1, end = n, freq = 1)

a.tt <- ts(a.tt, start = 1, end = n, freq = 1)

y <- ts(y, start = 1, end = n, freq = 1)

data <- cbind(alpha,a.tt,y)

# plot results

plot.ts(data, plot.type = c("single"), xlab = "iteration", ylab = "", lty = c(1,1,2), col = c("blue", "red", "green"), type = "l")

legend("topright", legend = c("true", "estimate", "measurement"), col = c("blue", "red", "green"), lty = c(1,1,3), bg = "white")

Below we can see the Kalman filter performs very well in this simple example.

 Note that we assumed the variances H and Q were known. In practice we would have to estimate these parameters using the data. The Kalman filter provides us with a way to form the likelihood and perform QMLE. I will address the problem of parameter estimation in Pt.2.