The paper is very short so I will only provide some of the key points and ask the interested reader to refer to the paper for the details.
Motivation
If the price ratio of two stocks is a mean reverting process then a simple pairs trading strategy could be to assume the ratio has a gaussian distribution and construct a 90% confidence interval and go long (short) the numerator stock, stock A, and go short (long) the denominator stock, stock B, when the price ratio rises above (falls below) the respective threshold. However, in practice the mean of the price ratio can often exhibit regime switches where the ratio stays high or low for sustained periods. This can lead to the basic pairs trading strategy outlined above performing poorly.
See Fig.1 for an illustration of sustained switches in the mean price ratio of two mining companies Anglo American and Xstrata.
 |
| Fig.1 |
The strategy outlined in Bock & Mestel's paper supposes that the price ratio of two stocks may follow a first-order markov-switching mean and variance process. This allows the trading rule to vary between regimes. For example in a high mean regime the variance of the ratio may be higher and so the 90% confidence interval for the high mean regime will be larger than the 90% confidence interval for the low mean regime.
Let
 denote the price ratio of stocks A and B.
denote the price ratio of stocks A and B.Then the price ratio is modelled as follows
where
and
Markov-switching relative value arbitrage rule
Bock & Mestel use the following trading rule
and
 indicates a short (long) position in stock A and a long (short) position in stock B, and
indicates a short (long) position in stock A and a long (short) position in stock B, and  indicates no position in either stock. We can see that in the case where the price ratio does not automatically identify the current regime, the algorithm uses the probabilities of each regime to decide whether a position should be taken. The probability threshold denoted by
indicates no position in either stock. We can see that in the case where the price ratio does not automatically identify the current regime, the algorithm uses the probabilities of each regime to decide whether a position should be taken. The probability threshold denoted by is chosen arbitrarily. Bock & Mestel suggest a probability threshold value between 0.6 and 0.7 so that the algorithm acts more cautiously in phases where the regime is not selective. The value of
is chosen arbitrarily. Bock & Mestel suggest a probability threshold value between 0.6 and 0.7 so that the algorithm acts more cautiously in phases where the regime is not selective. The value of can be interpreted as a sensitivity parameter which can be used to select the desired confidence level.
can be interpreted as a sensitivity parameter which can be used to select the desired confidence level.In what follows I consider two general mining companies Anglo American and Xstrata and apply the trading rule outlined above.
Assumptions
The daily close prices is used to calculate the price ratio. I assume that in practice that the price ratio is calculated using prices arbitrarily close to the end of the trading day e.g. 10 minutes before the end of the trading day and that buy or sell orders at the prevailing market price are executed at the market close price. Thus in calculating the returns from this strategy I assume that price of the two stocks do not change dramatically between the calculation of the price ratio and the execution of any required trades.
I also assume that the bid-ask spread is zero. This may significantly affect actual returns if the algorithm carries out a large number of trades.
Estimation
The Expectation Maximisation (EM) algorithm was used to obtain the Maximum Likelihood Estimates of the unknown parameters. I opted to repeat the EM algorithm a couple of times with random starting values to ensure the parameter estimates were stable.
Results
The following results are based on a 90% confidence interval for both regimes and a probability threshold value of 0.7.
The main plot in Fig.2 is a plot of the price ratio. The red regions indicate when the algorithm is betting that price ratio will decline, the blue regions indicate when the algorithm is betting on the price ratio increasing, and finally the green regions signal the algorithm not taking a position. The second plot in Fig.2 shows the smoothed probability that the series is in the high mean regime.
 |
| Fig.2 |
Fig.3 plots the returns from the strategy, a long-only strategy in the FTSE100, and long-only strategies in the individual stocks.
 |
| Fig.3 |
The unadjusted returns from this strategy look very impressive. It would be interesting to see what the returns would look like after adjusting for risk and bid-ask spreads.
Final thoughts
It is surprising the algorithm performs as well as it does given the model was only estimated using the previous year's data. Re-estimating the model half-way through the year incorporating more recent data might help to further improve the strategy's returns.
R code
########################################################
########################################################
######## MARKOV SWITCHING PAIR TRADING FUNCTIONS #######
########################################################
########################################################
# # # # # hamilton filter # # # # #
hamilton.filter <- function(theta, y, ss.prob, ps0=1/2, ps1=1/2) {
# construct parameters
mu_s0 <- theta[1]
mu_s1 <- theta[2]
sigma2_s0 <- exp(theta[3])
sigma2_s1 <- exp(theta[4])
gamma_s0 <- theta[5]
gamma_s1 <- theta[6]
# construct probabilities
#probit specification
p_s0_s0 <- pnorm(gamma_s0)
p_s0_s1 <- pnorm(gamma_s1)
p_s1_s0 <- 1-pnorm(gamma_s0)
p_s1_s1 <- 1-pnorm(gamma_s1)
# # # construct transition probability matrix P # # #
T.mat <- matrix(c(p_s0_s0, p_s1_s0, p_s0_s1, p_s1_s1), nrow = 2, ncol = 2, byrow = TRUE)
if(ss.prob == TRUE) {
# assume erogodicity of the markov chain
# use unconditional probabilities
p0_s0 <- (1 - p_s1_s1) / (2 -p_s0_s0 -p_s1_s1)
p0_s1 <- 1-p0_s0
}
else {
p0_s0 <- ps0
p0_s1 <- ps1
}
# create variables
n <- length(y)
p_s0_t_1 <- rep(0,n)
p_s1_t_1 <- rep(0,n)
p_s0_t <- rep(0,n)
p_s1_t <- rep(0,n)
f_s0 <- rep(0,n-1)
f_s1 <- rep(0,n-1)
f <- rep(0,n-1)
logf <- rep(0,n-1)
p_s0_t[1] <- p0_s0
p_s1_t[1] <- p0_s1
p_s0_t_1[1] <- p0_s0
p_s1_t_1[1] <- p0_s1
# initiate hamilton filter
for(i in 2:n) {
# calculate prior probabilities using the TPT
# TPT for this example gives us
# p_si_t_1 = p_si_t_1_si * p_si_t + p_si_t_1_sj * p_si_t
# where p_si_t_1 is the prob state_t = i given information @ time t-1
# p_si_t_1_sj is the prob state_t = i given state_t_1 = j, and all info @ time t-1
# p_si_t is the prob state_t = i given information @ time t
# in this simple example p_si_t_1_sj = p_si_sj
p_s0_t_1[i] <- (p_s0_s0 * p_s0_t[i-1]) + (p_s0_s1 * p_s1_t[i-1])
p_s1_t_1[i] <- (p_s1_s0 * p_s0_t[i-1]) + (p_s1_s1 * p_s1_t[i-1])
# calculate density function for observation i
# f_si is density conditional on state = i
# f is the density
f_s0[i] <- dnorm(y[i]-mu_s0, sd = sqrt(sigma2_s0))
f_s1[i] <- dnorm(y[i]-mu_s1, sd = sqrt(sigma2_s1))
f[i] <- (f_s0[i] * p_s0_t_1[i]) + (f_s1[i] * p_s1_t_1[i])
# calculate filtered/posterior probabilities using bayes rule
# p_si_t is the prob that state = i given information @ time t
p_s0_t[i] <- (f_s0[i] * p_s0_t_1[i]) / f[i]
p_s1_t[i] <- (f_s1[i] * p_s1_t_1[i]) / f[i]
logf[i] <- log(f[i])
}
logl <-sum(logf)
output <- list(p_s0_t_1 = p_s0_t_1, p_s1_t_1 = p_s1_t_1,f.prob_s0 = p_s0_t,f.prob_s1 = p_s1_t,T.mat = T.mat,logLik = logl)
return(output)
}
########################################################
########################################################
# # # # # Kim's smoothing algorithm # # # # #
kim.smooth <- function(T.mat,fp_s0,fp_s1,p_s0_t_1,p_s1_t_1) {
n <- length(fp_s0)
# create variables
p_s0_T <- rep(0,n)
p_s1_T <- rep(0,n)
p_s0_s0_t_1 <- rep(0,n-1)
p_s0_s1_t_1 <- rep(0,n-1)
p_s1_s0_t_1 <- rep(0,n-1)
p_s1_s1_t_1 <- rep(0,n-1)
# assign initial values to implement kim's algo
p_s0_T[n] <- fp_s0[n]
p_s1_T[n] <- fp_s1[n]
# initiate recursion
for(i in (n-1):1) {
p_s0_s0_t_1[i] <- fp_s0[i] * T.mat[1,1] * (p_s0_T[i+1]/p_s0_t_1[i+1])
p_s0_s1_t_1[i] <- fp_s0[i] * T.mat[1,2] * (p_s1_T[i+1]/p_s1_t_1[i+1])
p_s0_T[i] <- p_s0_s0_t_1[i] + p_s0_s1_t_1[i]
p_s1_s0_t_1[i] <- fp_s1[i] * T.mat[2,1] * (p_s0_T[i+1]/p_s0_t_1[i+1])
p_s1_s1_t_1[i] <- fp_s1[i] * T.mat[2,2] *(p_s1_T[i+1]/p_s1_t_1[i+1])
p_s1_T[i] <- p_s1_s0_t_1[i] + p_s1_s1_t_1[i]
}
output <- list(p_s0_s0_t_1 = p_s0_s0_t_1, p_s0_s1_t_1 = p_s0_s1_t_1, p_s1_s0_t_1 = p_s1_s0_t_1, p_s1_s1_t_1 = p_s1_s1_t_1, p_s0_T = p_s0_T, p_s1_T = p_s1_T)
return(output)
}
########################################################
########################################################
# # # # # EM algorithm # # # # #
EM <- function(y,tol,start_val) {
out <- hamilton.filter(start_val,y,ss.prob = TRUE)
fprob_s1 <- out$f.prob_s1
fprob_s0 <- out$f.prob_s0
p_s0_t_1 <- out$p_s0_t_1
p_s1_t_1 <- out$p_s1_t_1
T.mat <- out$T.mat
s.out <- kim.smooth(T.mat,fp_s0 = out$f.prob_s0 , fp_s1 = out$f.prob_s1, p_s0_t_1 = out$p_s0_t_1, p_s1_t_1 = out$p_s1_t_1)
p_s0_T <- s.out$p_s0_T
p_s1_T <- s.out$p_s1_T
p_s0_s0_t_1 <- s.out$p_s0_s0_t_1
p_s0_s1_t_1 <- s.out$p_s0_s1_t_1
p_s1_s0_t_1 <- s.out$p_s1_s0_t_1
p_s1_s1_t_1 <- s.out$p_s1_s1_t_1
# first iteration of the transition probabilities
p00_k <- sum(p_s0_s0_t_1) / sum(p_s0_T[2:length(p_s0_T)])
p01_k <- sum(p_s0_s1_t_1) / sum(p_s1_T[2:length(p_s1_T)])
# recall we used a probit parameterization for the probabilities so we need to backout gamma_s0 and gamma_s1
gamma_s0_k <- qnorm(p00_k)
gamma_s1_k <- qnorm(p01_k)
# calculate first iteration of parameters
mu_s0_k <- (sum(p_s0_T))^(-1) * sum(y * p_s0_T)
mu_s1_k <- (sum(p_s1_T))^(-1) * sum(y * p_s1_T)
sigma2_s0_k <- sum( (y-mu_s0_k)^2 * p_s0_T ) / sum(p_s0_T)
sigma2_s1_k <- sum( (y-mu_s1_k)^2 * p_s1_T ) / sum(p_s1_T)
theta_k <- rbind(mu_s0_k,mu_s1_k,log(sigma2_s0_k),log(sigma2_s1_k),gamma_s0_k,gamma_s1_k)
# measure the distance between new estimates and initial values
x <- theta_k-start_val
dist <- crossprod(x)
# use theta_k becomes theta_k_1 to compute next iteration
theta_k_1 <- theta_k
# count iterations
count <- 1
# start_val given in the following order (mu_s0,mu_s1,sigma2_s0,sigma2_s1,gamma_s0,gamma_s1)
while(dist > tol) {
out <- hamilton.filter(theta_k_1,y,ss.prob = TRUE)
fprob_s1 <- out$f.prob_s1
fprob_s0 <- out$f.prob_s0
p_s0_t_1 <- out$p_s0_t_1
p_s1_t_1 <- out$p_s1_t_1
T.mat <- out$T.mat
s.out <- kim.smooth(T.mat,fp_s0 = out$f.prob_s0 , fp_s1 = out$f.prob_s1, p_s0_t_1 = out$p_s0_t_1, p_s1_t_1 = out$p_s1_t_1)
p_s0_T <- s.out$p_s0_T
p_s1_T <- s.out$p_s1_T
p_s0_s0_t_1 <- s.out$p_s0_s0_t_1
p_s0_s1_t_1 <- s.out$p_s0_s1_t_1
p_s1_s0_t_1 <- s.out$p_s1_s0_t_1
p_s1_s1_t_1 <- s.out$p_s1_s1_t_1
# iteration of the transition probabilities
p00_k <- sum(p_s0_s0_t_1) / sum(p_s0_T[2:length(p_s0_T)])
p01_k <- sum(p_s0_s1_t_1) / sum(p_s1_T[2:length(p_s1_T)])
# recall we used a probit parameterization for the probabilities so we need to backout gamma_s0 and gamma_s1 using qnorm()
gamma_s0_k <- qnorm(p00_k)
gamma_s1_k <- qnorm(p01_k)
# calculate first iteration of parameters
mu_s0_k <- (sum(s.out$p_s0_T))^(-1) * sum(y * p_s0_T)
mu_s1_k <- (sum(s.out$p_s1_T))^(-1) * sum(y * p_s1_T)
sigma2_s0_k <- sum( (y-mu_s0_k)^2 * p_s0_T ) / sum(p_s0_T)
sigma2_s1_k <- sum( (y-mu_s1_k)^2 * p_s1_T ) / sum(p_s1_T)
theta_k <- rbind(mu_s0_k,mu_s1_k,log(sigma2_s0_k),log(sigma2_s1_k),gamma_s0_k,gamma_s1_k)
# measure the distance between new estimates and initial values
x <- theta_k - theta_k_1
dist <- crossprod(x)
# use theta_k becomes theta_k_1 to compute next iteration
theta_k_1 <- theta_k
# count iterations
count <- count + 1
}
final.out <- hamilton.filter(theta_k,y,ss.prob = TRUE)
rownames(theta_k) <-c("mu_s0", "mu_s1", "log(sigma2_s0)", "log(sigma2_s1)", "gamma_s0", "gamma_s1")
result <- list(theta_k = theta_k, distance = dist, tolerance = tol, no.iter = count, logLik = final.out$logLik, T.mat = final.out$T.mat)
return(result)
}
########################################################
########################################################
# # # # # trade signalling function # # # # #
trade.signal <- function(ratio,mle.pars,prob_s0,prob_s1,delta,rho) {
# ratio = Pa_t/Pb_t
n <- length(ratio)
st <-rep(0,n)
high_state <- which.max(mle.pars[1:2])
low_state <- which.min(mle.pars[1:2])
if(high_state == 1) {
high_sd <- exp(mle.pars[3])
low_sd <- exp(mle.pars[4])
prob_high <- prob_s0
prob_low <- prob_s1
}
else {
high_sd <- exp(mle.pars[4])
low_sd <- exp(mle.pars[3])
prob_high <- prob_s1
prob_low <- prob_s0
}
for(i in 1:n) {
if((ratio[i] < mle.pars[high_state] - delta * high_sd) && prob_high[i] > rho) {
st[i] <- 1
}
if(ratio[i] > mle.pars[high_state] + delta * high_sd) {
st[i] <- -1
}
if((ratio[i] > mle.pars[low_state] + delta * low_sd) && prob_low[i] > rho) {
st[i] <- -1
}
if(ratio[i] < mle.pars[low_state] - delta * low_sd) {
st[i] <- 1
}
st <- zoo(st, index(ratio))
}
return(st)
}
########################################################
########################################################
# # # # backtest function # # # #
back.test <- function(benchmark,numerator,denominator,signal) {
require(quantmod)
n <- length(signal)
num_signal <-rep(0,n)
denom_signal <- rep(0,n)
for(i in 1:n) {
if(signal[i] == 1) {
num_signal[i] <- 1
denom_signal[i] <- -1
}
if(signal[i] == -1) {
num_signal[i] <- -1
denom_signal[i] <- 1
}
}
num_signal <- zoo(num_signal, index(signal))
denom_signal <-zoo(denom_signal, index(signal))
x <- zoo(0,index(signal[1]))
nsig <- rbind(x,lag(num_signal, k =-1))
dsig <- rbind(x,lag(denom_signal, k =-1))
benchmark.ret <- dailyReturn(benchmark, type = c("log"))
numerator.ret <- dailyReturn(numerator, type = c("log"))
denominator.ret <- dailyReturn(denominator, type = c("log"))
benchmark.ret <- as.zoo(benchmark.ret)
numerator.ret <- as.zoo(numerator.ret)
denominator.ret <- as.zoo(denominator.ret)
strat_return <- exp(cumsum(numerator.ret*nsig)+cumsum(denominator.ret*dsig))
benchmark_return <- exp(cumsum(benchmark.ret))
numerator_return <- exp(cumsum(numerator.ret))
denominator_return <- exp(cumsum(denominator.ret))
return(list(numerator_signal = nsig, denominator_signal = dsig,benchmark_return = benchmark_return,numerator_return = numerator_return, denominator_return = denominator_return, strat_return = strat_return))
}
########################################################
########################################################
########################################################
########################################################
########################################################
########################################################
############ IMPLEMENTATION OF THE STRATEGY ############
########################################################
########################################################
library(quantmod)
# # # # # # # # # # get stock price data # # # # # # # # # #
getSymbols("AAL.L", from = "2010-01-01", to = "2011-01-01")
getSymbols("XTA.L", from = "2010-01-01", to = "2011-01-01")
aal.2010 <- Cl(AAL.L)
xta.2010 <- Cl(XTA.L)
# # calculate price ratios # #
price.ratio.2010 <- aal.2010/xta.2010
# # # # # # # # # # parameter estimation # # # # # # # # # #
# pick start values for the 6 unknown parameters
# k is the number of times the EM algorithm is run
# different starting values for each run
k <- 5
start_val <- matrix(rnorm(6*k), nrow = 6, ncol = k)
# matrix to store parameter estimates
par.cand <- matrix(NA,nrow = 6, ncol = k)
# row vector to store likelihood values
like.cand <- matrix(NA, nrow = 1, ncol = k)
for(i in 1:k) {
x <-try(EM(price.ratio.2010,tol = 1e-24,start_val[,i]))
if(class(x) == "try-error") next
par.cand[,i] <- x$theta_k
like.cand[,i] <-x$logLik
cat("Iteration", i, "of", k, "\n")
}
results <- rbind(like.cand,par.cand)
# # # select mle from candidates # # #
like.cand <- results[1,]
index <- which.max(like.cand)
mle.pars <- results[-1,index]
# # # identify which regime is the high mean regime # # #
which.max(mle.pars[1:2])
# # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # #
# # # get filtered probabilities # # #
output <- hamilton.filter(mle.pars,price.ratio.2010,ss.prob = TRUE)
fprob_s0.2010 <- output$f.prob_s0
fprob_s1.2010 <- output$f.prob_s1
p_s0_t_1.2010 <- output$p_s0_t_1
p_s1_t_1.2010 <- output$p_s1_t_1
# # # get transition matrix # # #
T.mat <- output$T.mat
# # # get smoothed probabilities # # #
smoothed.output <- kim.smooth(T.mat,fprob_s0.2010,fprob_s1.2010,p_s0_t_1.2010,p_s1_t_1.2010)
p_s0_T.2010 <- smoothed.output$p_s0_T
p_s1_T.2010 <- smoothed.output$p_s1_T
# # # # # # # # # # get data for this year # # # # # # # # # #
getSymbols("AAL.L", from = "2011-01-02")
getSymbols("XTA.L", from = "2011-01-02")
getSymbols("^FTSE", from = "2011-01-02")
aal.2011 <- Cl(AAL.L)
xta.2011 <- Cl(XTA.L)
ftse.2011 <- Cl(FTSE)
# calculate new.price.ratio
price.ratio.2011 <- aal.2011/xta.2011
# get filtered probabilities for new data
# # # get filtered probabilities for new data # # #
output2 <- hamilton.filter(mle.pars,price.ratio.2011,ss.prob = TRUE)
fprob_s0.2011 <- output2$f.prob_s0
fprob_s1.2011 <- output2$f.prob_s1
p_s0_t_1.2011 <- output2$p_s0_t_1
p_s1_t_1.2011 <- output2$p_s1_t_1
# # # get transition matrix # # #
T.mat.2011 <- output2$T.mat
# # # get smoothed probabilities # # #
smoothed.output2 <- kim.smooth(T.mat.2011,fprob_s0.2011,fprob_s1.2011,p_s0_t_1.2011,p_s1_t_1.2011)
p_s0_T.2011 <- smoothed.output2$p_s0_T
p_s1_T.2011 <- smoothed.output2$p_s1_T
# get signal
signal <- trade.signal(ratio = price.ratio.2011, mle.pars, prob_s0 = p_s0_T.2011,prob_s1 = p_s1_T.2011,delta = 1.645,rho = 0.7)
# backtest model
bt.results <- back.test(ftse.2011,numerator=aal.2011,denominator=xta.2011,signal)
# # # # # # # # plot results # # # # # # # #
# plot returns
plot.zoo(merge(bt.results$strat_return, bt.results$benchmark_return, bt.results$numerator_return, bt.results$denominator_return),plot.type = c("single"), col = c("red", "blue", "green", "yellow"), ylab = "", xlab = "Date", main = "Continuously Compounded Returns (2011-01-04 to 2011-12-23)")
legend("topleft", legend = c("strategy","ftse","aal","xta"), col = c("red", "blue", "green", "yellow"), lty = 1, bty = "n")
# plot price ratio and trading signals
chartSeries(price.ratio.2011,name = "Price Ratio of AAL.L - XTA.L", theme = chartTheme("black"))
plot(addTA(signal > 0, border = NA, col = "blue", on = -1))
plot(addTA(signal == 0, border = NA, col = "green", on = -1))
plot(addTA(signal < 0, border = NA, col = "red", on = -1))
addTA(zoo(p_s1_T.2011,index(price.ratio.2011)), legend = "Smoothed probability of high regime")



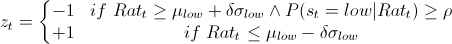

I ran the same code a number of times and observed that the graphs for smoothed probability of high regime varied exactly complimentarily....that is the in one graph, the regions which showed high prob the next graph showed low prob.....n the inversion was same in every region...can you explain what is happening here?
ReplyDeletehere are the two plots:
ReplyDeletehttps://docs.google.com/file/d/0BytuJt-JzVVjSnNndVdhYk9qUjA/edit?usp=sharing
https://docs.google.com/file/d/0BytuJt-JzVVjX2JDLVRKNWdWM2s/edit?usp=sharing
Hi N,
ReplyDeleteCould we have quick email chat about your code?
xmoon2000@googlemail.com